Training GANs the right way

Welcome to my first blog post! I am years overdue in doing this. To preface things a bit:

Updates:

If you found this useful and wish to cite it, you can use this corresponding Bibtex entry:

@misc{beckhamc_traininggans,
  author = {Beckham, Christopher},
  title = {Training {GAN}s the right way},
  year = {2021},
  publisher = {GitHub},
  journal = {GitHub repository},
  howpublished = {\url{https://beckham.nz/2021/06/28/training-gans.html}}
}

Table of contents

The key ingredient to stabilising GAN training

GAN training used to involve a lot of heuristics in order to minimise their various degenerate behaviours, like mode collapse or mode dropping. Commonly this meant setting up the generator and discriminator in such a way that the latter did not perform ‘too well’, because that would ultimately mean risking vanishing or exploding gradients from the discriminator. The worst degenerate behaviour is when the generator exhibits mode collapse, in which the model outputs the same image no matter what input its given. The other behaviour, mode dropping, also isn’t ideal because it means there are certain factors of variation in the data distribution that fail to get modelled. Despite the fact that we try to do our best to minimise this behaviour, I would argue here that GANs exhibit mode dropping behaviour by design. This is because GANs optimise something that isn’t identical to maximum likelihood, which is inherently mode covering and is the mechanism by which autoencoders are trained. (See [#ref:colin].)

In 2017 the Wasserstein-GAN (WGAN) [#ref:wgan] was published and made some very interesting theoretical and empirical contributions to GANs and adversarial training, most notably in stabilising them and making them significantly less of a hassle to train. To summarise the paper – and I hope I don’t butcher this explanation – the gist of the paper is that:

Therefore, the key thing is to somehow ensure that the discriminator is \(K\)-Lipschitz (for some small \(K\)). In the original paper this was done via (1) weight clipping technique, and in later literature this was followed by (2) gradient penalty [#ref:wgan_gp] and then (3) spectral normalisation [#ref:sn]. A quick summary of these is that (1) is overly excessive in its regularisation, (2) is rather expensive to compute and only penalises certain parts of the function, and (3) regularises the entire function and is rather cheap to compute. In particular, spectral norm[#ref:sn] ensures that the Lipschitz constant of the network is upper bounded by one (1-Lipschitz), by constraining the largest singular value for each weight matrix in the discriminator network to be equal to one. We’ll talk about that later, but for now let’s go back to basics.

To briefly summarise WGAN [#ref:wgan], via the Kantorovich-Rubenstein (KR) duality, the Wasserstein distance between two distributions can be expressed as the following:

\[W(P_r, P_{\theta}) = \sup_{||D||_{L} \leq 1} \mathbb{E}_{x \sim P_r} D(x) - \mathbb{E}_{x \sim P_{\theta}} D(x),\]

where \(P_r\) refers to the real distribution and \(P_{\theta}\) the generator’s distribution, and \(D(x) \in \mathbb{R}\). Unlike the original paper, I am using \(D(\cdot)\) to denote the discriminator (critic) instead of \(f(\cdot)\). The supremum is basically saying that the Wasserstein distance corresponds to the function \(D\) that makes the following term as large as possible, i.e. make \(\mathbb{E}_{x \sim P_r} D(x)\) very large and \(\mathbb{E}_{x \sim P_{\theta}} D(x)\) very small. Equivalently, modifying the supremum so that it instead is over \(K\)-Lipschitz functions simply amounts to multiplying the distance by the scaling factor \(K\), i.e:

\[K \cdot W(P_r, P_{\theta}) = \sup_{||D||_{L} \leq K} \mathbb{E}_{x \sim P_r} D(x) - \mathbb{E}_{x \sim P_{\theta}} D(x).\]

While we obviously cannot compute such a supremum, the basic idea is to just enforce that Lipschitz constraint on \(D\) and treat it as a network that simply approximates the true Wasserstein distance. Quite simply, \(W\) is the loss that the discriminator tries to maximise, while the generator tries to minimise it. In other words, \(D\) tries to maximise the (approximated Wasserstein) distance between the real and generated distributions, while \(G\) tries to make them as similar as possible. Therefore, we can write \(D\) and \(G\)’s losses as:

\[\begin{align} \mathcal{L}_{D} & = \max_{D} \ \ \ \ \ \mathbb{E}_{x \sim P_r} D(x) - \mathbb{E}_{x \sim P_{\theta}} D(x) \\ & = \min_{D} \underbrace{\mathbb{E}_{x \sim P_{\theta}} D(x)}_{\text{make as small as possible}} - \underbrace{\mathbb{E}_{x \sim P_r} D(x)}_{\text{make as large as possible}} \\ \mathcal{L}_{G} & = \min_{G} - \underbrace{\mathbb{E}_{x \sim P_{\theta}} D(x)}_{\text{make as large as possible}} \end{align}\]

Note that for \(D\) I am writing its loss both as a maximisation and a minimisation (which is just the negative of the maximisation). The former is convenient if you want to think about the two networks’ losses in terms of a minimax game, but the latter is more convenient for an actual implementation since we tend to minimise loss functions in code. Let us briefly compare this to JS-GAN’s formulation, which is sort of similar but involving logs and a sigmoid nonlinearity on \(D\):

\[\begin{align} \mathcal{L}_{D} & = \max_{D} \mathbb{E}_{x \sim P_r} \log \sigma(D(x)) + \mathbb{E}_{x \sim P_{\theta}} \log(1 - \sigma(D(x))) \ \ \ \text{(1)} \\ & = \max_{D} \mathbb{E}_{x \sim P_r} \log D_r(x) - \mathbb{E}_{x \sim P_{\theta}} \log(D_f(x)) \ \ \ \text{(2)}, \\ \end{align}\]

where in (1) \(\sigma(\cdot)\) denotes the sigmoid nonlinearity. In the following line I have decided to define two outputs on \(D\) instead (\(D_r\) for probability of real and \(D_f\) for probability of fake, as if this was a two-class softmax) so that we can remove the sigmoid term and turn the summation term in (1) into a subtraction in (2) to be more reminiscent of WGAN’s loss. Finally, the log function can just be thought of as a non-linearity as well.

The reason for this little comparison is because it segways into an interesting detail that Martin Arjovsky wrote in the WGAN appendix. He says that, ultimately, a JS-GAN is quite similar to WGAN if you also apply similar Lipschitz constraints:


Figure 1: Interesting appendix detail about JSGAN, found in the supplementary material from WGAN.

I find this interesting, though what certainly muddies the waters a bit is that there evidence to suggest that in practice a Lipschitz’d JS-GAN performs better than a Lipschitz’d WGAN:

Maybe it’s a mystery for now, but if it’s any consolation, theoretically both the regularised JSGAN and WGAN formulations are very similar and in practice you should just use JS-GAN, or even better, the hinge loss proposed in [#ref:sn]. Spectral normalisation has been in PyTorch for quite some time now, and it’s as simply as wrapping each linear and conv layer in your discriminator with torch.nn.utils.spectral_norm:

import torch
from torch import nn

# spec norm is built into pytorch, and it's very
# plug and play
from torch.nn.utils import spectral_norm as spec_norm

n_in = 10
n_out = 20

layer_l = spec_norm(nn.Linear(n_in, n_out))

layer_c = spec_norm(nn.Conv2d(n_in, n_out, kernel_size=3))

Prior to this work, these were many tricks that I saw on how to stabilise GAN training [#ref:gan_hacks]. While I don’t want to say that none of these have any utility anymore whatsoever, I have not had to use any of these. I feel however that any newcomers may stumble across such things and not realise that there are more straightforward ways to train GANs now.

Figure 2: Some GAN training hacks I stumbled across on this Github repo. These tricks date back five years and probably many of these tricks are not needed anymore.


Structuring the code cleanly

Clean code makes it easier to find bugs and reason about your code. Good abstractions are part of that. I like to have a train_on_batch(x) method, which performs a single gradient step over the batch x. Since GANs are a two-player game between \(G\) and \(D\) however, how do we structure the code? Which network should we train first?

Personally, I perform the gradient steps for the generator first, i.e., the \(G\) step. But it doesn’t matter which way you do it, as long as you’re careful as to how you’re handling the gradients. I’m going to be writing PyTorch-inspired pseudo-code (it’s using Python and PyTorch syntax but it’s not meant to be run per se, not unless you define a bunch of variables and implement the undefined methods I have written).

####################################################################
# This code is not meant to be executed -- it's simply pseudocode. #
####################################################################

REAL = 1
FAKE = 0

def train_on_batch(x_real):
    
    opt_g.zero_grad()
    opt_d.zero_grad()
    
    # --------------
    # First, train G
    # --------------
    
    z = sample_z(x_real.size(0))
    x_fake = G(z)
    g_loss = gan_loss( D(x_fake), REAL)
    # This backpropagates from the output of D, all the
    # way back into G.
    g_loss.backward()
    # G's gradient buffers are filled, we can perform
    # an optimisation step.
    opt_g.step()
    
    # ------------
    # Now, train D
    # ------------
    
    # IMPORTANT: D's grad buffers are filled because
    # of what we did above.
    opt_d.zero_grad()
    
    # x_fake.detach() not necessary here but it stops
    # grads from backpropagating into G. Even if that
    # did happen howwever, the start of `train_on_batch` 
    # zeros both gradient buffers anyway, so it doesn't 
    # matter.
    d_loss = gan_loss( D(x_fake.detach()), FAKE) + \
             gan_loss( D(x_real), REAL )
    d_loss.backward()
    opt_d.step()
    
    return g_loss.detach(), d_loss.detach()

What if you want to do it the other way around? Easy, though I find it’s a bit more confusing:

####################################################################
# This code is not meant to be executed -- it's simply pseudocode. #
####################################################################

REAL = 1
FAKE = 0

def train_on_batch(x_real):
    
    opt_g.zero_grad()
    opt_d.zero_grad()
    
    # ------------
    # Now, train D
    # ------------

    z = sample_z(x_real.size(0))
    x_fake = G(z)
    
    # Call `x_fake.detach()` because we don't want to
    # backpropagate gradients into G. If you didn't
    # use detach(), then when you call `g_loss.backward()`
    # later on you'd have to supply `retain_graph=True`.
    # Let's not do such confusing things...
    d_loss = gan_loss( D(x_fake.detach()), FAKE) + \
             gan_loss( D(x_real), REAL )
    d_loss.backward()
    opt_d.step()
    
    # ------------
    # Now, train G
    # ------------
    
    opt_d.zero_grad()
    
    g_loss = gan_loss( D(x_fake), REAL)
    # This backpropagates from the output of D, all the
    # way back into G.
    g_loss.backward()
    # G's gradient buffers are filled, we can perform
    # an optimisation step.
    opt_g.step()
    
    return g_loss.detach(), d_loss.detach()

You may see in some GAN implementations the use of backward(retain_graph=True) in order to be able to backprop through a particular graph more than once. For instance, in the code block directly before this you would have to use retain_graph=True if I didn’t detach() the tensor x_fake for the block that trains D. I have avoided such use of that here since I personally find it more confusing to think about.

Why have I defined a function gan_loss here? Because for certain GAN formulations (like JS-GAN), it helps a lot with readability. Rather than doing this, which can be relatively less readable and more error prone:

d_loss = -log(D(x_real)) - log(1-D(x_fake))
g_loss = -log(D(x_fake))

You could instead just write (at the expense of a few extra lines):

bce = nn.BCELoss()

# 1 = real, 0 = fake
ones = torch.ones((x_real.size(0), 1)).float()
zeros = torch.zeros_like(ones)

d_loss = bce( D(x_real), ones ) + bce( D(x_fake), zeros )
g_loss = bce( D(x_fake), ones )

Easy or common pitfalls to make

Plot your damn learning curves!

Most of the time when people come to me with GAN problems, they never come with graphs included and I usually have to ask for it. Sometimes I get no immediate response, and I wonder if it’s because they have to write code to do it, which certainly implies that their workflow isn’t very plotting-centric. Pessimistically it makes me wonder if the way most people debug things in deep learning is to just look at metrics flying down the terminal screen like this:

EPOCH: 001, TRAIN_D_LOSS: 0.4326436, TRAIN_G_LOSS: 1.352356, TIME: 435.353 SEC ...
EPOCH: 002, TRAIN_D_LOSS: 0.4521224, TRAIN_G_LOSS: 1.325623, TIME: 425.353 SEC ...
EPOCH: 003, TRAIN_D_LOSS: 0.4575744, TRAIN_G_LOSS: 1.657234, TIME: 422.533 SEC ...
EPOCH: 004, TRAIN_D_LOSS: 0.4025356, TRAIN_G_LOSS: 1.124543, TIME: 411.632 SEC ...
EPOCH: 005, TRAIN_D_LOSS: 0.4235636, TRAIN_G_LOSS: 1.457234, TIME: 450.353 SEC ...
...
...
...
(continue until your eyes get sore)

While our field does seem like the polar opposite of classical statistics (i.e. simple linear models, interpretability, etc.), we do have something in common with classical statistics, and that is in exploratory analysis. Just like classical statistics, deep learning should involve lots of exploratory analysis. Sure, that exploration isn’t going to be on 10,000-dimensional data (we can only see in three dimensions), but it will be on variables that your model is either optimising or measuring, which is extremely important to monitor if you want to know your network is training correctly. In our case, the losses are d_loss and g_loss, as defined in earlier pseudocode.

In Figure 3 I have illustrated these curves, left for a regular JS-GAN and on the right a spectrally normalised variant, SN-GAN.

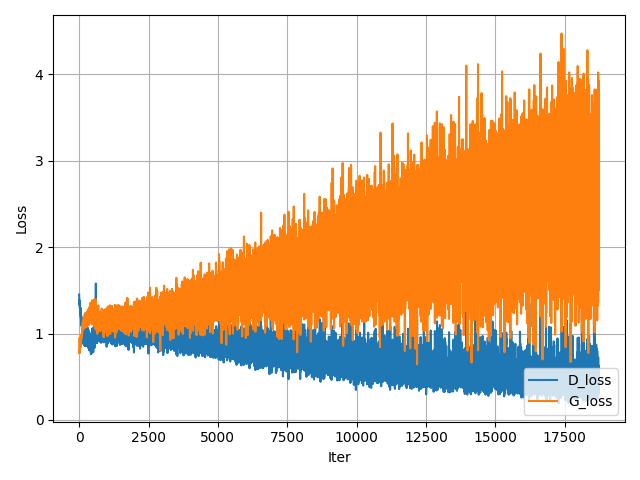
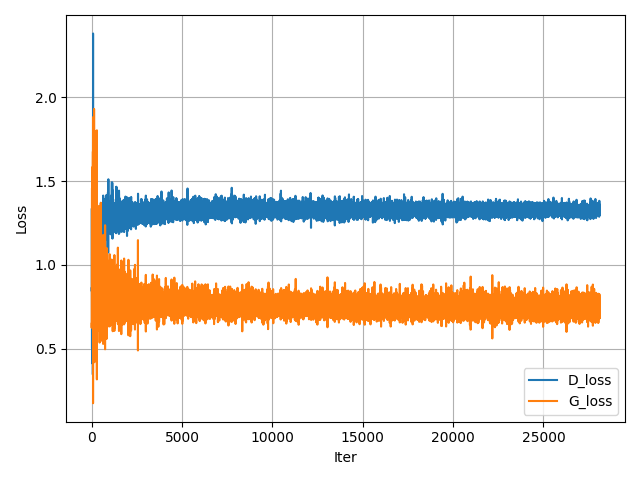
missing missing
Figure 3. Left: Unregularised JS-GAN; right: JS-GAN regularised with spectral normalisation ('SN-GAN'). Note that the discriminator loss is unnormalised and should be divided by 2 here, since it constitutes two terms (the real and the fake terms). In that case, for the right-most figure the generator and discriminator losses for SN-GAN are roughly the same value, though typically over time they will diverge very slowly. It does seem that this phenomena completely contradicts the 'Nash equilibrium' theory of GANs, which says that -- theoretically -- both networks should converge to the same loss, implying that neither network is able to reach a lower loss by fooling the other. This seems to generally not happen in practice. For more details on why, you can consult [[#ref:nash]](#ref_nash).

In my experience training SN-GAN (not JS-GAN), you want to be in a regime where the D loss is lower than the G loss but not by ‘too much’. For instance, if one loss is much larger or smaller than the other, this may be indicative of something problematic. For instance, if d_loss << g_loss (where << = significantly lower), this could mean your generator does not have enough capacity to model the data well and cannot compete well with the discriminator. Alternatively, if g_loss << d_loss, the discriminator may not be powerful enough, either. While you could use some sort of ‘balancing’ heuristic like roughly make both networks have the same # of learnable parameters, this is actually really crude. For instance, it’s expected \(G\) have way more parameters than \(D\) since it’s actually trying to model the data distribution (rather than simply distinguish between the two), so it doesn’t exactly set off alarm bells if your discriminator is only 5M parameters and your generator is 50M. Also, a 50M network with heavy weight decay does not have the same modeling capacity as one without it. Lastly, the issue certainly may not be in model complexity but rather the training dynamics. For example, if either network is really deep, are you making use of residual skip connections? If you’re concerned with vanishing gradients, you could also plot the average gradient norms here).

This is one of these things you will get a feel for after training lots of GANs. My best advice is to look at existing implementations of GANs on Github (ones that achieve good performance) and use their architectures as a base for your own work.

Because of Lipschitz, you don’t need to cripple your discriminator

Based on what I said about K-Lipschitz, it should certainly help (and not degrade gradients in any way) to give your discriminator a head start by training it for relatively more iterations than the generator. In other words, the better the discriminator is at distinguishing between real and fake, the better the signal that the generator can leverage from it. Note that as I mentioned earlier in this article, this logic did not make sense in the ‘pre-WGAN’ days because making the discriminator too good was detrimental to training.

In my own code, I simply keep track of the iteration number so that I can compute something like the following:

def train_on_batch(x, iter_, n_gen=5):
    # Generator
    ...
    ...
    if iter_ % n_gen == 0:
        g_loss.backward()
        opt_g.step()
        
    # Disc
    ...
    ...
    d_loss.backward()
    d_loss.step()

Where iter_ is the current gradient step iteration, and n_gen defines the interval between generator updates. In this case, since it’s 5, we can think of this as meaning that the discriminator is updated 5x as much as the generator.

Other people may do something like the following, preferring to leverage the data loader to perform such a thing:

def train(N):
    
    # number of discriminator iters per
    # generator iter
    n_dis = 5

    for iteration in range(N):

        for x_real in data_loader:
            # Update G
            train_on_batch_g(x_real)

        for _ in range(n_dis):
            for x_real in data_loader:
                # Update D
                train_on_batch_d(x_real)

Optimisers

The only optimiser I’ve really used for GANs is ADAM, and it seems like everyone else does as well. I don’t know why it works so well, but maybe it’s because all of our models have evolved over time to perform well on ADAM [#ref:adam_evolve], even if it may not necessarily be the right optimiser to always use.

[#ref:sn] presents a neat paper on various ADAM hps that they tried out, and which ones gave the best Inception scores:

missing
Figure 4: barplot illustrating ideal ADAM hyperparameters over different GAN parameterisations. (Taken from spectral norm paper)

As one can see here, for SN-GAN, option (C) performs best for CIFAR10 and option (B) for STL-10. Unfortunately however, as that graph shows, you can get wildly different optimal hps depending on what kind of GAN variant you are working with. In my own experience, I have found betas=(0, 0.9), lr=2e-4 to be a reasonable starting point.

Pesky hyperparameter: ADAM’s epsilon

ADAM’s default epsilon parameter in PyTorch is 1e-8, which may cause issues after a long period of training, such as your loss periodically exploding or increasing. See the StackOverflow post here as well as the Reddit comments here.

There may be some alternatives that alleviate this issue, such as Adamax. But I have not tried using it yet with GAN training.

Evaluation metrics

The two most commonly used metrics are Inception and FID, though there have been a whole host of other ones proposed as well. Unfortunately, these metrics can often be rather frustrating to use, and I will detail as many reasons as I can for this below.

Here are some things you should keep in mind about FID:

There are other problems too. See ‘A note on the inception score’ [5] for a comprehensive critique of these scores.

Either way, you should be monitoring these metrics during training, as opposed to simply training the GAN for a fixed number of epochs and evaluating them afterwards. Think about this as being no different from training a classifier and monitoring its validation set accuracy during training: you want to know if image quality is improving over time, and you want to know if you’re able to stop training early when the FID/Inception plateaus or gets worse. Since these metrics can be expensive to compute, set up your code so that the metrics are computed every few epochs, so that you don’t completely bottleneck your training time.

Which is the best?

Ultimately, I feel like whatever evaluation metric you use really depends on what your downstream task is. If you just want to generate pretty images then sure, use something like FID or Inception. If however you are using GANs for something like data augmentation, then an appropriate metric would be training a classifier on that augmented data and seeing how well it performs on a held-out set.

While GANs are great in many aspects, one of their biggest downsides is not having a theoretically straightforward way of evaluating likelihoods. VAEs more or less give you this, by allowing you to compute a lower bound on \(p(x)\).

Conditioning on more than one noise variable

Sometimes you may want to train a more flexible generator, one that is able to be conditioned on more than one noise variable. For instance, rather than \(G(z)\) you may want \(G(z, c)\), where \(c \sim p(c)\) comes from some other prior distribution, e.g. a Categorical distribution. If you train the GAN, you will most likely find that it completely ignores one noise variable and uses the other.

In order to resolve this, you should turn to InfoGAN [#ref:infogan]. Put simply, the discriminator should have two additional output branches, one to predict both latent codes fed into the generator, and you should train the discriminator to be able to predict these codes from the generated image. In other words, we want to maximise the mutual information between the original codes input \((z, c)\) and the generated image \(G(z, c)\). One caveat however, we actually want to minimise such a loss with respect to both generator and discriminator; so this loss isn’t adversarial per se, but more like a ‘cooperative’ loss that both networks have to minimise. Here is some pseudo-code, assuming \(p(c)\) here is a Categorical distribution:

def train_on_batch(x):

  opt_d.zero_grad()
  opt_g.zero_grad()
  # or opt_all.zero_grad()

  c = sample_c(x.size(0))
  z = sample_z(x.size(0))

  # generator loss
  x_fake = G(z, c)
  ...
  ...
  # discriminator loss
  d_realfake, _, _ = D(x_fake)
  ...
  ...

  # `opt_all` wraps both the generator
  # and discriminator parameters, since we
  # we want to minimise the infogan loss
  # wrt to both networks.
  opt_all.zero_grad()
  # imagine D has three output layers: one
  # to determine real/fake, and the other two
  # for our noise variables.
  _, d_out_c, d_out_z = D(x_fake)
  z_loss = torch.mean((d_out_z-z)**2)
  # you could also use mean squared error here,
  # but i'm using the x-entropy to be more correct
  # about it, since p(c) is a multinomial distribution.
  # this means that `d_out_c` has been transformed with
  # the softmax nonlinearity.
  c_loss = categorical_crossentropy(d_out_c, c).mean()
  infogan_loss = z_loss + c_loss
  infogan_loss.backward()
  opt_all.step()

Resources

Conclusion

If you think I’ve missed something or you’ve spotted an error, please let me know in the comments section at the bottom of this page or reach out to me on Twitter!

References

Appendix

The relationship between PyTorch and TF Inception scores

import pandas as pd
import matplotlib.pyplot as plt
%matplotlib inline

df = pd.read_csv("./incep_tf_vs_pt.csv", names=["pytorch", "tensorflow"])
df
pytorch tensorflow
0 6.78 7.68
1 6.82 7.63
2 6.75 7.68
3 6.73 7.40
4 6.63 7.48
5 6.85 7.81
6 6.29 7.24
7 6.92 7.66
8 7.03 7.63
9 6.98 7.62
10 7.18 7.81
11 6.80 7.60
12 6.79 7.63
13 7.01 7.76
14 7.03 7.84
15 6.25 7.02
16 6.82 7.62 
from sklearn import linear_model
import numpy as np
lm = linear_model.LinearRegression()

X = df['pytorch'].values.reshape(-1, 1)
y = df['tensorflow'].values.reshape(-1, 1)

lm.fit(X, y)

plt.scatter(X, y)
plt.ylabel('tensorflow IS')
plt.xlabel('pytorch IS')

xs = np.linspace(6, 7.5, num=100).reshape(-1, 1)
ys = lm.predict(xs)
plt.plot(xs, ys)
plt.grid()
lm_str = "y = %.2fx + %.2f" % (lm.coef_[0][0], lm.intercept_[0])
plt.title(lm_str)